The Ballpark Strategy: Estimation as a Practical Problem-Solving Tool

Beyond Exact Calculation: The Power of Approximation

In a world obsessed with precision, the ballpark strategy offers a liberating alternative. Rather than pursuing exact calculations through lengthy arithmetic, ballparking allows you to estimate answers through intelligent approximation—a technique that is not only faster but often more reliable in real-world problem-solving contexts.

To “ballpark” is to estimate roughly, to think about numerical figures in a practical, common-sense manner rather than pursuing mathematical exactitude. The Business Dictionary defines it as “an approximation made with a degree of knowledge and confidence that the estimated figure falls within a reasonable range of values.”

This strategy is particularly valuable in quantitative problem-solving because it combines speed with accuracy while eliminating many common calculation errors.

Why Ballparking Works

Most multiple-choice quantitative problems include deliberately distracting options designed to catch computational errors or misunderstandings. By ballparking, you accomplish two critical objectives simultaneously:

1. Eliminate clearly wrong answers — Once you’ve estimated the reasonable range for the answer, you can immediately discard options that fall far outside this range.

2. Identify the correct answer through logic — Rather than grinding through calculations to arrive at an exact answer, you can often identify which option falls within the reasonable ballpark range.

Example 1: Percentage Calculation

Question: What is 32.33% of 50?

Options:

1. 5.125
2. 16.165
3. 35.685
4. 50.350
5. 70.195

The numbers appear intimidating, and a test-taker might feel overwhelmed contemplating the calculations required. This emotional response is precisely what the question is designed to trigger, increasing the likelihood of computational errors.

Ballpark Approach:

Notice that 32.33% is very close to 1/3 (which equals approximately 33.33%). The calculation becomes simple: 1/3 of 50 is slightly more than 16.

Looking at the options, only Option B (16.165) falls within this reasonable range. This is your answer.

Alternative ballpark approach:

Approximate 32.33% as 30% to simplify mental calculation. Now: (30/100) × 50 = 15. Since you approximated downward (using 30% instead of 32.33%), the actual answer should be slightly higher than 15.

Option B at 16.165 is the only choice reasonably close to 15 and accounts for the upward adjustment. Confirmed.

Example 2: Complex Fraction Operations

Question: Which of the following is nearest to a complex fraction expression?

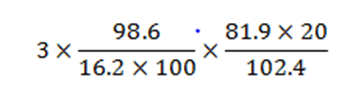
Options:

1. 15
2. 10
3. 7
4. 3
5. 1

When faced with a complex fraction containing multiple decimal values, the impulse to calculate exactly is overwhelming. But this plays directly into the question’s design—to see if you’ll waste time in calculation and potentially make arithmetic errors.

Ballpark Approach:

Rather than working with decimals, round them to nearby whole numbers. Convert the complex fraction into simpler integer operations that you can perform mentally.

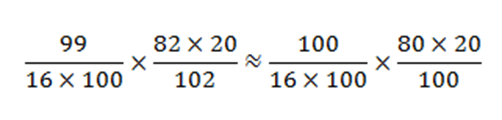
After this simplification, your rough calculation yields approximately 1. But here’s the critical detail: the original expression had a coefficient of 3. Therefore, the final answer is approximately 3 × 1 = 3 (Option D).

If you had stopped at your intermediate calculation of 1, you would have incorrectly selected Option E. The ballpark strategy succeeds not by eliminating thought but by combining rough calculation with careful attention to the original problem structure.

Core Principles of Effective Ballparking

1. Identify convenient approximations

• Recognize that 32.33% is close to 1/3
• Notice that 51% is approximately 1/2
• See that 9.99 is essentially 10

2. Replace complexity with simplicity

• Convert decimals to whole numbers when possible
• Substitute awkward fractions with familiar benchmarks
• Simplify operations mentally before reaching for paper

3. Maintain directionality awareness

• When you round downward, your answer should be higher than your estimate
• When you round upward, your answer should be lower than your estimate
• This directional awareness helps you select among close options

4. Read carefully to avoid trap choices

• Complex problems may have coefficients or multipliers you must not forget
• Ballparking saves calculation time only if you maintain attention to the full problem structure
• The speed advantage disappears if it creates careless errors

When to Use Ballparking

This strategy is most effective when:

• Dealing with intimidating numbers — When the quantities look complex or the calculations appear lengthy, ballparking often provides a faster, cleaner path to the answer.
• Working under time pressure — The method reduces calculation time significantly, allowing you to allocate effort to more challenging problems.
• Eliminating options — Even when you’re uncertain of the exact answer, ballparking typically narrows the field to one or two plausible options.
• Verifying calculated answers — After solving a problem through traditional methods, ballparking provides a sanity check. If your calculated answer falls way outside the ballpark range, you know an error occurred.

When to Avoid Pure Ballparking

However, ballparking should not be your default strategy in all situations:

• When precision is explicitly required — Some problems demand exact answers, and approximation is simply insufficient.
• When answer choices are close together — If options are clustered (e.g., 15.2, 15.5, 15.8), ballparking alone cannot differentiate between them.
• When you can solve quickly and accurately — If the direct calculation is straightforward, there’s no advantage to approximation.

Developing Ballparking Proficiency

Like any problem-solving technique, ballparking becomes more natural and reliable with practice. As you work through problems, you’ll develop:

• Intuition for common approximations — You’ll recognize at a glance that 49 is close to 50, that 0.33 equals approximately 1/3, that 0.25 equals 1/4.
• Sensitivity to order of magnitude — You’ll quickly estimate whether an answer should be in the single digits, tens, hundreds, or higher.
• Confidence in rough estimates — Rather than viewing approximation as “cheating” or inferior to exact calculation, you’ll recognize it as a legitimate, efficient problem-solving method.

Conclusion: Strategic Approximation as Intellectual Discipline

The ballpark strategy represents a sophisticated approach to quantitative reasoning. It’s not about being imprecise or lazy; it’s about applying intelligence strategically. By estimating reasonably and eliminating implausible options, you solve problems faster while reducing the computational errors that plague exact calculation under time pressure. In a world where speed and accuracy both matter, ballparking offers a practical middle path—capturing the benefits of both while minimizing the drawbacks of either approach alone.